设在美国的电子新领域基金会为寻找梅森素数开出了“悬赏金”,最少也有10万美元——180多个国家和地区超过22万人参加了“因特网梅森素数大搜索”(GIMPS)国际合作项目,动用了40多万台计算机联网来进行大规模“搜捕”。什么是梅森素数?梅森素数为何那样火爆?
欧几里德的谜题
素数也叫质数,是只能被1和自身整除的数,如2、3、5、7等等。公元前300多年,古希腊数学家欧几里德用反证法证明了素数有无穷多个,他还提出有少量素数可以写成2p-1(其中指数P为素数)的形式。
究竟有多少个素数可以写成这种形式?欧几里德把这个问题留给了后人。于是,费马、笛卡尔、哥德巴赫、欧拉、高斯……几乎所有大数学家都研究过这种特殊形式的素数,17世纪的法国数学家马林·梅森是其中成果最为卓著的一位。
梅森学识渊博、才华横溢,是法兰西科学院的奠基人和当时欧洲科学界的中心人物。为了纪念他,数学界就把2p-1型的数称为“梅森数”,并以Mp记之;如果Mp为素数,则称之为“梅森素数”。
然而,2300多年来,人类仅发现47个梅森素数。这种素数新奇而迷人,因此有“数学珍宝”的美誉。梅森素数历来是数论研究的一项重要内容,也是当今科学探索的热点和难点之一。
梅森素数的价值
别以为寻找梅森素数只是数学家们的消遣和游戏,梅森素数在当代具有十分丰富的理论意义和实用价值。它是发现已知最大素数的最有效途径,它的探究推动了数学皇后——数论的研究,促进了计算技术、程序设计技术、密码技术、网格技术的发展以及快速傅立叶变换的应用。另外,梅森素数的探究方法还可用来测试计算机硬件运算是否正确。
许多科学家认为,由于梅森素数的探究需要多种学科和技术的支持,它的研究成果在一定程度上反映了一个国家的科技发展水平。英国顶尖科学家、牛津大学教授马科斯·索托伊甚至认为它是“人类智力发展在数学上的一种标志,也是科学发展的里程碑”。
寻找梅森素数的艰难之旅
在“手算笔录”年代,人们历尽艰辛,仅找到12个梅森素数。电子计算机的出现,大大加快了探究梅森素数的步伐。1952年美国数学家拉斐尔·鲁滨逊等人将著名的卢卡斯-雷默方法编译成计算机程序,使用SWAC型计算机在5个月之内,就找到了5个梅森素数:M521、M607、M1279、M2203和M2281。
然而对人们来讲,梅森素数却仍然是个谜。梅森素数是不是无穷的?梅森素数有什么分布规律?从已发现的梅森素数来看,它在正整数中的分布时疏时密、极不规则,因此研究梅森素数的分布规律似乎比寻找新的梅森素数更为困难。
英、法、德、美等国的数学家都曾分别给出过有关梅森素数分布的猜测,但这些猜测都是“近似”的,没有准确的表达式,都在实践中显出了瑕疵,折戟沉沙。中国数学家和语言学家周海中是这方面研究的领先者——他运用联系观察法和不完全归纳法,于1992年首次给出了梅森素数分布的精确表达式。后来这项重要成果被国际上命名为“周氏猜测”。《科学》杂志有一篇文章指出:周氏猜测为人们探究梅森素数提供了方便,是素数研究的一项重大突破。
信息技术带来新希望
让我们再回到GIMPS这个国际项目。1996年初,美国数学家和程序设计师乔治·沃特曼编制了一个梅森素数计算程序,并把它放在网页上供全球数学家和业余数学爱好者免费下载使用——这就是举世闻名的GIMPS项目,它采取网格计算方式,把大量普通计算机的闲置时间“团结”起来,获得相当于超级计算机的运算能力。
为了推动梅森素数的寻找,也为了促进网格技术的发展,设在美国的电子新领域基金会(EFF)开始了“悬赏”。1999年3月,基金会向全世界宣布:向第一个找到超过1000万位数的个人或机构颁发10万美元;超过1亿位数,15万美元;超过10亿位数,25万美元。当然,绝大多数研究者参与该项目并不是为了金钱,而是出于好奇心、荣誉感和探索精神。
就在最近,10万美元名花有主。2008年8月23日,美国加州大学洛杉矶分校的计算机专家埃德森·史密斯发现了迄今已知的最大梅森素数M43112609,该数也是目前已知的最大素数。这个素数有12978189位;如果用普通字号将它连续写下来,长度可超过50公里!这一重大成就被著名的《时代》杂志评为“2008年度50项最佳发明”之一。不过,史密斯是私自利用学校的75台计算机参加GIMPS项目的。本来这种行为应该被处罚,但鉴于他为学校争了光,因而受到了校方的表彰。
另一位仁兄就没有这样的运气。美国一家电话公司的雇员麦克·福雷斯特偷偷地使用公司内的2585台计算机参加GIMPS项目;随后公司发现计算机经常会出些差错,本来只需要5秒钟就可以接通的电话号码,需要5分钟才能接通。联邦调查局最终查到了原因,福雷斯特承认“被GIMPS项目引诱”;他最后被解雇,并被罚款一万美元。
15年来,人们通过GIMPS项目找到了13个梅森素数,其发现者来自美国、英国、法国、德国、加拿大和挪威。目前该项目的计算能力已超过当今世界上任何一台最先进的超级矢量计算机的计算能力,运算速度达到每秒650万亿次。著名的《自然》杂志说:GIMPS项目不仅会进一步激发人们对梅森素数寻找的热情,而且会引起人们对网格技术应用研究的高度重视。(文内图片为资料图片)
■链接
梅森素数趣闻
梅森素数貌似简单,但不仅需要高深的理论和纯熟的技巧,还需要进行艰巨的计算。1772年,有“数学英雄”美称的欧拉在双目失明的情况下,靠心算证明了M31(即231-1=2147483647)是一个素数。该素数有10位,堪称当时世界上已知的最大素数。欧拉的毅力与技巧都令人赞叹不已,难怪法国大数学家皮埃尔·拉普拉斯向他的学生们说:“读读欧拉,他是我们每一个人的老师。”
梅森素数的探究不仅极富挑战性,而且对研究者来说有一种巨大的荣誉感。1963年6月2日晚上8点,当第23个梅森素数M11213通过大型计算机被找到时,美国广播公司(ABC)中断了正常的节目播放,在第一时间发布了这一重要消息。发现这一素数的美国伊利诺伊大学数学系全体师生感到无比骄傲,他们甚至把所有从系里发出的信封都盖上了“211213-1是个素数”的邮戳。
随着素数P值的增大,每一个梅森素数Mp的产生都艰辛无比;而科学家及业余研究者们仍乐此不疲,激烈竞争。例如,在1979年2月23日,当美国克雷研究公司的计算机专家大卫·史洛温斯基和哈里·纳尔逊宣布他们找到第26个梅森素数M23209时,有人告诉他们:在两星期前美国加州的高中生兰登·诺尔就已经给出了同样结果。为此他们潜心发奋,又花了一个半月的时间,使用Cray-1型计算机找到了新的梅森素数M44497。这件事成了当时不少主流报纸的头版新闻。



 上一版
上一版



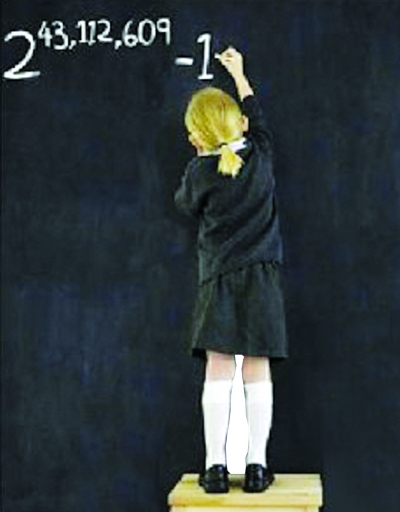
 缩小
缩小 全文复制
全文复制